How to Calculate Weighted Average: Step-by-Step Guide (+ Examples)

Understanding how to calculate a weighted average is crucial for unlocking insights from complex data sets.

Unlike a simple average, which treats every value equally, a weighted average assigns varying levels of importance to different data points, ensuring that more significant values have a greater influence on the result. This makes weighted averages a more accurate and meaningful measure, particularly in fields like grading systems, financial markets, and business data analysis.

In this article, you will learn how to calculate weighted averages and understand their practical applications.

Key Takeaways:

• Weighted averages help to give more importance to certain data points, offering a more accurate representation of a dataset.
• To calculate a weighted average, multiply each value by its corresponding weight, sum the products, and divide by the total of the weights.
• Weighted averages are widely used in academics, finance, and business to calculate grades, portfolio returns, and costs.

By mastering the concept of weighted averages, you’ll be able to apply this technique to real-world scenarios with ease. For those new to math, tips on how to learn algebra can significantly help in grasping the fundamentals and applying them to weighted averages.

What Is a Weighted Average?

A weighted average is a calculation that accounts for the varying importance of each number in a dataset. Unlike a simple average (or arithmetic mean), which treats all values equally, the weighted average assigns a specific weight to each value before summing them. This ensures that more significant numbers have a greater influence on the final result, making it a more accurate representation of the data.

Weighted averages are widely used in many fields. In education, they help calculate students’ grades by assigning different weights to assignments, exams, and participation. In finance, weighted averages assess the performance of investment portfolios, weighing each investment according to its market value. Inventory management also relies on weighted averages to calculate the cost of goods sold, factoring in varying costs and quantities.

Similarly, calculating the nth term of a sequence is another important concept in mathematics that involves understanding how individual terms in a series relate to one another.

This flexibility makes weighted averages a vital tool in fields ranging from academics to business, providing more precise and insightful analysis.

Simple vs. Weighted Average

A simple average (or arithmetic mean) is calculated by summing all the values in a dataset and dividing the result by the number of values. This method assumes that every value in the dataset has equal importance.

For example, if you have three test scores—90, 80, and 70—the simple average is:

$$\text{Simple Average}=\frac{90+80+70}{3}=80$$

On the other hand, a weighted average accounts for the varying importance of each value in the dataset. Each value is multiplied by a specific weight, reflecting its significance, and the weighted average is calculated by dividing the sum of these weighted values by the total of the weights.

For example, if the same test scores have different weights—say, 50% for the first test, 30% for the second, and 20% for the third—the weighted average would be:

$$\text{Weighted Average}=\frac{(90\times 0.50)+(80\times 0.30)+(70\times 0.20)}{0.50+0.30+0.20}=83$$

As you can see, the weighted average takes into account the relative importance of each test score, providing a more accurate reflection of the overall performance.

In summary, the key difference is that a simple average treats all values equally, while a weighted average gives different importance to each value based on its weight, leading to more accurate insights when values vary in significance.

Basic Concepts

Understanding basic concepts of averages is essential in many fields, from statistics to everyday decision-making. The simple average, also known as the arithmetic mean, is calculated by summing a group of numbers and dividing by the total count. This method works well for datasets with relatively consistent values, where each value is treated equally.

However, a weighted average is more appropriate when values have different levels of importance or weight. To calculate the weighted average, multiply each number by its respective weight, then divide the sum of these products by the sum of the weights.

The difference between a simple average and a weighted average can be best illustrated with an example.

Imagine a student’s grade in a course, where the final exam is worth 60% and coursework contributes 40%. If the student scores 90 in coursework and 80 on the final exam, the weighted average would be calculated as follows:

(0.4 × 90) + (0.6 × 80) = 84.

This reflects the different importance of each component.

In contrast, a simple average would treat both components equally, giving:

(90 + 80) / 2 = 85,

which doesn’t account for the exam’s higher weight.

How to Calculate a Weighted Average

Statistical analysis often relies on the concept of a weighted average, which provides a clearer picture when not all values in a data set are of equal significance. The weighted average formula takes into account the relative importance (weight) of each value in the final result.

The formula for calculating a weighted average is as follows:

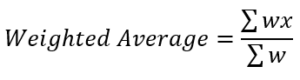
Where:

• xi​ represents each value in the data set;
• wi​ represents the weight of each value.

Step 1: Identify the values and their corresponding weights.Start by listing all the values (denoted as xi) and assign a weight (wi​) to each. These weights reflect the relative importance or frequency of each value in the data set.

Step 2: Multiply each value by its weight. For each value, multiply it by its corresponding weight to calculate the weighted contribution of that value.

Step 3: Sum up all the products obtained from step 2. Add up all the weighted products from the previous step to get the total weighted sum.

Step 4: Sum up all the weights. Next, add together all the weights (wi​) to get the total weight sum.

Step 5: Divide the sum of products by the sum of weights to find a weighted average. Finally, divide the total weighted sum by the total sum of weights to calculate the weighted average.

Detailed Weighted Average Example

Let’s walk through a detailed example to calculate a weighted average:

Suppose we have three products with different prices and sales volumes. We want to find the average price, but each product has a different sales volume, so we need to use a weighted average.

• Product A: Price = $10, Units Sold = 100
• Product B: Price = $20, Units Sold = 200
• Product C: Price = $30, Units Sold = 50

1. Identify values and weights

Values (prices): $10, $20, $30
Weights (units sold): 100, 200, 50

2. Multiply each value by its weight

• $10 * 100 = $1000
• $20 * 200 = $4000
• $30 * 50 = $1500

3. Sum up all the products:

$1000 + $4000 + $1500 = $6500

4. Sum up all the weights:

100 + 200 + 50 = 350

5: Divide the sum of products by the sum of weights

$$\frac{6500}{350} \approx 18.57$$

So, the weighted average price of the products, considering the units sold, is $18.57. This gives a more accurate representation of the average price per product sold, as it accounts for the volume of sales for each product.

Practical Examples

Academic Grading

In education, a student’s final grade is often determined by various components such as assignments, exams, and participation, each with its own weight. For example, 30% of the grade might come from assignments, 50% from tests, and 20% from participation.

Let’s calculate the weighted average for a student who scores:

• 85 on assignments
• 90 on tests
• 95 on participation

The formula for the weighted mean grade would look like this:

$$\text{Weighted Mean Grade}=\frac{(85\times 0.30)+(90\times 0.50)+(95\times 0.20)}{0.30+0.50+0.20}$$

Breaking it down:

• (85×0.30)=25.5
• (90×0.50)=45
• (95×0.20)=19

Now sum them up:

$$\text{Weighted Mean Grade} = \frac{25.5 + 45 + 19}{1} = 89.5$$

 

So, the student’s final weighted grade would be 89.5, reflecting the different weights of each academic component.

Financial Analysis

In finance, a key concept is the Weighted Average Cost of Capital (WACC). Let’s consider a company that has:

• 60% equity at a cost of 8%
• 40% debt at a cost of 4%

To calculate the WACC, use the weighted average formula:

$$\text{WACC}=(0.60\times 0.08)+(0.40\times 0.04)$$

Breaking it down:

• 0.60×0.08=0.048
• 0.40×0.04=0.016

Now sum them up:

$$\text{WACC}=0.048+0.016=0.064\text{ or }6.4\mathrm{\%}$$

This weighted figure is crucial for making decisions about investments and financing.

Survey Analysis

In survey analysis, different questions might carry varying levels of importance. Let’s say:

• Question 1 has a weight of 1 and an average score of 4.0
• Question 2 has a weight of 2 and an average score of 3.5

To calculate the overall weighted average for the survey:

$$\text{Weighted Average Opinion}=\frac{(4.0\times 1)+(3.5\times 2)}{1+\mathrm{2<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;"></span>}}$$

Breaking it down:

• (4.0×1)=4.0
• (3.5×2)=7.0

Now sum them up:

$$\text{Weighted Average Opinion}=\frac{4.0+7.0}{3}=3.67$$

This weighted average gives a more nuanced view of the survey responses, reflecting the varying significance of each question.

Tips and Common Mistakes

When calculating a weighted average, it’s crucial to assign the correct weights to each value. These weights should accurately reflect the significance of each value in the dataset. An error in assigning weights can lead to incorrect conclusions, so it’s important to double-check your criteria for assigning weights. If needed, consult with a peer or a research paper writing help for validation.

Common mistakes to avoid:

• Misaligned Values and Weights:
  A common mistake when working with large datasets is having the values and their corresponding weights out of sync. Always ensure each value is paired with the correct weight. To help stay organized, consider using a table to match each value with its weight.
• Incorrect Summing of Products and Weights:
  Mistakes can occur when summing the weighted products or weights. Using a calculator or spreadsheet software can significantly reduce the chances of errors. If you’re unsure, always check your calculations step by step.
• Rounding Issues:
  Rounding numbers too early in the process can impact the accuracy of your final weighted average, especially with large datasets or when precision is required. It’s best to perform calculations with raw numbers and only round off at the very end. If rounding mid-calculation is necessary, keep the number of decimal places consistent to reduce rounding errors over time.

When making critical decisions, always double-check your calculations and maintain a record of the original, unrounded numbers for future reference.

Applications of Weighted Average

Weighted averages are indispensable in a wide range of fields and use cases. Here are just a few examples:

• Economics: Weighted averages are crucial for calculating indices such as the Consumer Price Index (CPI), where different goods are weighted based on their significance in consumer spending patterns.
• Finance: In finance, weighted averages are used to determine portfolio returns, taking into account the varying stakes of different investments. They are also key in calculating the Weighted Average Cost of Capital (WACC), which is essential for corporate financial strategies.
• Education: In academic settings, weighted averages help calculate a student’s GPA by considering the credit hours and difficulty level of courses.
• Healthcare: In health data analysis, weighted averages are used to account for factors like the severity or frequency of medical conditions.
• Sports: In sports, player statistics (such as a quarterback’s rating) often use weighted averages to provide a more accurate performance measure.

These examples highlight the importance of weighted averages in offering a more nuanced understanding of data and ensuring that each piece of information contributes appropriately to the final analysis.

Tools and Software for Calculating Weighted Average

Tools like Microsoft Excel and Google Sheets make calculating weighted averages fast and easy, reducing the risk of human error. Here’s how you can use them:

In Excel:

•  The SUMPRODUCT function combined with the SUM function is a powerful way to calculate the weighted average. For example, you could use this formula:

=SUMPRODUCT(B2:B10, C2:C10) / SUM(C2:C10)

Where B2:B10 contains your values and C2:C10 contains the corresponding weights.

In Google Sheets:

• Google Sheets offers the same functionality as Excel. You can use the SUMPRODUCT formula to calculate the weighted average easily. The formula structure remains the same.

These tools update dynamically, so if any data points or weights change, the weighted average is automatically recalculated, ensuring you always have the most accurate results.

If you’re looking to deepen your understanding of weighted averages and other mathematical concepts, exploring the best online math courses can provide you with a structured, comprehensive approach to mastering these useful tools and techniques.

The Bottom Line

Weighted averages are essential for more accurate analysis across various industries, including finance, education, and business. They allow for a more precise reflection of data by giving more weight to significant values. While calculating a weighted average is more complex than using a simple average, it provides a more accurate and insightful result.

For those looking to deepen their understanding of this concept, online math courses can offer a structured approach to mastering weighted averages and other key mathematical tools. Investing time in learning these concepts can enhance your ability to make more informed decisions and apply these methods in a wide range of practical situations.